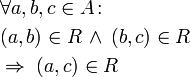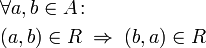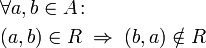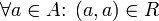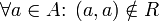Object Property Axioms
Object properties link individuals to individuals.
A set of instances connected to the property is called a property extension.
Contents
- 1 SubObjectPropertyOf axiom
- 2 Equivalent object property axiom
- 3 Inverse object properties axiom
- 4 Disjoint object properties axiom
- 5 Functional object properties axiom
- 6 Inverse functional object properties axiom
- 7 Transitive object property axiom
- 8 Symmetric object property axiom
- 9 Asymmetric object property axiom
- 10 Reflexive object property axiom
- 11 Sources
SubObjectPropertyOf axiom
This axiom says that a property 'p1' is a subproperty 'sp1' of another property 'p2'. It also means that the instances of the subproperty are subsets to the property extension of the second property.
Equivalent object property axiom
Equivalent property axioms exist, when two properties have the same property extension.
Inverse object properties axiom
Properties have a direction defined with domain to range, the 'inverseof' term is used to mirror the direction.
This Axiom can equally be used on object properties and data properties.
Disjoint object properties axiom
Two properties are disjoint when they don't have individuals in common.
Functional object properties axiom
A functional property is a property which can only have one value.
For an individual 'x', there can be only one definite individual 'y' such that 'x' is connected by the object property expression 'OPE' to 'y'.
For example: FunctionalObjectProperty( a:hasHusband ) Each object can have at most one husband. ObjectPropertyAssertion( a:hasHusband a:Nicole a:Steve ) Steve is Nicole's husband.
Inverse functional object properties axiom
For an individual 'x', there can be at most one individual 'y' such that 'y' is connected by the object property expression 'OPE' with 'x'.
InverseFunctionalObjectProperty( a:hasHusband ) Each object can have at most one husband. ObjectPropertyAssertion( a:hasHusband a:Steve a:Nicole ) Steve is Nicole's husband.
Transitive object property axiom
Transitive means that if a property contains the pair(x,y)and the pair (y,z) then we can conclude that the pair(x,z) is also part of der property.
Symmetric object property axiom
If a property is symmetric it means that if a pair(x,y) exists, then there is also a pair (y,x).
Asymmetric object property axiom
A asymmetric property has a pair(x,y) but never a pair(y,x).
Reflexive object property axiom
Reflexive means that a property relates to itself.
Irreflexive object property axiom
Subsequently irreflexive means that no individual relates to itself.
Object property domain axiom
This axiom states that the domain of the object property expression is the class expression.
Object property range axiom
This axiom states that the range of the object property expression is the class expression.
SubPropertyChainOf axiom
These axioms are used to create a chain of multiple properties. E.g. two 'hasParents' properties are linked by a chain thus a 'hasGrandparents' property will be identified.