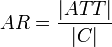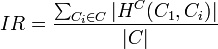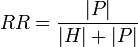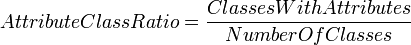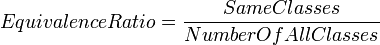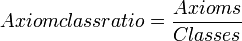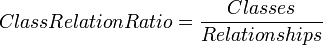Schema Metrics

Schema metrics address the design of the ontology. Although we cannot definitely know if the ontology design correctly models the domain knowledge, metrics in this category indicate the richness, width, depth, and inheritance of an ontology schema design. The most significant metrics in this category are described next.

Attribute Richness

The number of attributes (slots) that are defined for each class can indicate both the quality of ontology design and the amount of information pertaining to instance data. In general we assume that the more slots that are defined the more knowledge the ontology conveys.

The attribute richness (AR) is defined as the average number of attributes (slots) per class. It is computed as the number attributes for all classes (att) divided by the number of classes (C).

$AR = \dfrac{|ATT|}{|C|}$

Note: Usually, only the functional attributes are counted to calculate this metric, as stated in the OWL definition. In our metric calculation, we omit this restriction and use all declared attributes to calculate, because not many modellers use the possibility of defining functional attributes. Also, the datatype are being handled as attributes as well.

Inheritance Richness

Inheritance Richness (IR) measure describes the distribution of information across different levels of the ontology’s inheritance tree or the fan-out of parent classes. This is a good indication of how well knowledge is grouped into different categories and subcategories in the ontology. This measure can distinguish a horizontal ontology (where classes have a large number of direct subclasses) from a vertical ontology (where classes have a small number of direct subclasses). An ontology with a low inheritance richness would be of a deep (or vertical) ontology, which indicates that the ontology covers a specific domain in a detailed manner, while an ontology with a high IR would be a shallow (or horizontal) ontology, which indicates that the ontology represents a wide range of general knowledge with a low level of detail.

The inheritance richness of the schema (IR) is defined as the average number of subclasses per class. The number of subclasses of a class is defined as 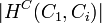$|H^C(C_1,C_i)|$. H is the number of inheritance relationships.

$IR = \frac{\sum_{C_i \in C}|H^C(C_1,C_i)|}{|C|}$

Relationship Richness

This metric reflects the diversity of the types of relations in the ontology. An ontology that contains only inheritance relationships usually conveys less information than an ontology that contains a diverse set of relationships. The relationship richness is represented as the percentage of the (non-inheritance) relationships between classes compared to all of the possible connections that can include inheritance and non-inheritance relationships.

The relationship richness (RR) of a schema is defined as the ratio of the number of (non-inheritance) relationships (P), divided by the total number of relationships defined in the schema (the sum of the number of inheritance relationships (H) and non-inheritance relationships (P)).

$RR = \frac{|P|}{|H|+|P|}$

Note: The following relationships are being counted as non-inherited relationships: Object Properties, Equivalent Classes, Disjoint Classes.

The subclasses (Subclasses of) are being handled as inheritance relationships.

Attribute-Class Ratio

This metric represents the relation between the classes containing attributes and all classes. The difference to attribute richness is that not the amount of attributes is counted. It is only counted whether a class has attributes or not.

$AttributeClass Ratio=\frac{Classes With Attributes}{Number Of Classes}$

Equivalence Ratio

This metric calculates the ratio between similar classes and all classes in the ontology.

It is being calculated as follows:

$Equivalence Ratio =\frac{Same Classes}{Number Of All Classes}$

Axiom Class Ratio

This metric describes the ratio between axioms and classes. It is calculated as the average amount of axioms per class.

$Axiom class ratio=\frac{Axioms}{Classes}$

Inverse Relations Ratio

This metric describes the ratio between the inverse relations and all relations. It is calculated as follows:

$Inverse Relations Ratio = \frac{Inverse Object Properties + Inverse Functional Data Properties}{All Object Properties + All Functional Data Properties}$

Class Relation Ratio

This metric describes the ratio between the classes and the relations in the ontology.

$Class Relation Ratio =\frac{Classes}{Relationships}$

Note: The following ontology components are counted as relationships: Object Properties, Equivalent Classes, Disjoint Classes, Subclasses(Subclass of).

Sources

1. Samir Tartir, I. Budak Arpinar, Amit P. Sheth: Ontological Evaluation and Validation
   In: Theory and Applications of Ontology: Computer Applications 2010, pp 115-130.
   http://link.springer.com/chapter/10.1007%2F978-90-481-8847-5_5
2. Aldo Gangemi, Carola Catenacci, Massimiliano Ciaramita, Jos Lehmann:
   Ontology evaluation and validation - An integrated formal model for the quality diagnostic task
   September 2005, pp 19-20.
   http://www.loa.istc.cnr.it/old/Files/OntoEval4OntoDev_Final.pdf