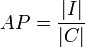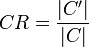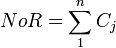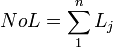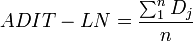Knowledgebase Metrics

The way data is placed within an ontology is also a very important measure of ontology quality because it can indicate the effectiveness of the ontology design and the amount of real-world knowledge represented by the ontology. Instance metrics include metrics that describe the knowledgebase as a whole, and metrics that describe the way each schema class is being utilized in the knowledgebase.

Average Population

(The average distribution of instances across all classes)

This measure is an indication of the number of instances compared to the number of classes. It can be useful if the ontology developer is not sure if enough instances were extracted compared to the number of classes.

Formally, the average population (AP) of classes in a knowledgebase is defined as the number of instances of the knowledgebase (I) divided by the number of classes defined in the ontology schema (C).

$AP=\frac{|I|}{|C|}$

The result will be a real number that shows how well is the data extraction process that was performed to populate the knowledgebase. For example, if the average number of instances per class is low, when read in conjunction with the previous metric, this number would indicate that the instances extracted into the knowledgebase might be insufficient to represent all of the knowledge in the schema. Keep in mind that some of the schema classes might have a very low number or a very high number by the nature of what it is representing.

Source 1

Class Richness

This metric is related to how instances are distributed across classes. The number of classes that have instances in the knowledgebase is compared with the total number of classes, giving a general idea of how well the knowledgebase utilizes the knowledge modelled by the schema classes. Thus, if the knowledgebase has a very low Class Richness, then the knowledgebase does not have data that exemplifies all the class knowledge that exists in the schema. On the other hand, a knowledgebase that has a very high class richness would indicate that the data in the knowledgebase represents most of the knowledge in the schema.

The class richness (CR) of a knowledgebase is defined as the percentage of the number of non-empty classes (classes with instances) (C') divided by the total number of classes (C) defined in the ontology schema.

$CR= \frac{|C'|}{|C|}$

Source 1

Cohesion

This metric is not implemented in the ontometrics project yet.

The cohesion shows the degree of relatedness between the different entities. When the entities of an ontology are highly related there is a strong cohesion value.

To be able to measure the cohesion three different metrics will be used:

Number of root classes (NoR)

Same as Absolute Root Cardinality in Graph Metrics!

Displays the number of root classes of an ontology, a root class is a class which is not a sub class of any other class in the ontology. 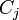$C_j$ is the jth root class.

 $NoR= \sum _{1}^n C_j$

Number of leaf classes (NoL)

Same as Absolute Leaf Cardinality in Graph Metrics!

Displays the number of leaf classes of an ontology, a leaf class doesn't have any sub classes. 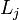$L_j$ is the jth leaf class.

$NoL= \sum_{1}^n L_j$

Average depth of inheritance tree of leaf nodes (ADIT-LN)

Same as Average Depth in Graph Metrics!

It is the sum of the depth of all paths divided by the total number of paths (n). The total number of paths is the number of paths from each root node to each leaf node. while the depth is the total number of nodes starting with the root node, ending with the leaf node of one path. 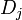$D_j$ is the total number of nodes on the path j.

$ADIT-LN= \frac{\sum_{1}^n D_j} {n}$

Source 2

Sources

1. Samir Tartir, I. Budak Arpinar, Michael Moore, Amit P. Sheth, and Boanerges Aleman-meza:
   Ontoqa: Metric-based ontology quality analysis.
   In: IEEE Workshop on Knowledge Acquisition from Distributed, Autonomous, Semantically Heterogeneous Data and Knowledge Sources, 2005, p 4.
   http://cobweb.cs.uga.edu/~budak/papers/ontoqa.pdf
2. Aldo Gangemi, Carola Catenacci, Massimiliano Ciaramita, Jos Lehmann:
   Ontology evaluation and validation - An integrated formal model for the quality diagnostic task
   September 2005 , pp 44-45.
   http://www.loa.istc.cnr.it/old/Files/OntoEval4OntoDev_Final.pdf