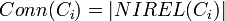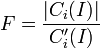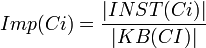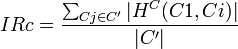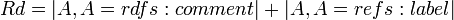Difference between revisions of "Class Metrics"
Adminofwiki (Talk | contribs) |
Adminofwiki (Talk | contribs) |
||
| (26 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
<math>Conn(C_i)=|NIREL(C_i)|</math> | <math>Conn(C_i)=|NIREL(C_i)|</math> | ||
| + | |||
| + | [[Class_Metrics#Sources | Source 1]] | ||
==Class Fullness== | ==Class Fullness== | ||
| − | This metric details the knowledgebase average population metric | + | This metric details the knowledgebase average population metric which are part of the [[Knowledgebase_Metrics | knowledgebase metrics]]. It would be mainly used by an ontology developer interested in knowing how well the data extraction was with respect to the expected number of instances of each class. This is helpful in directing the extraction process to any resources that will add instances belonging to classes that are not full. |
| − | Formally, the '''fullness (F)''' of a '''class <math> C_i</math>''' is defined as the actual number of instances that belong to the subtree rooted at <math>C_i (C_i (I))</math> compared to the expected number of instances that belong to the subtree rooted at <math>C_i (C_i'(I))</math>. | + | Formally, the '''fullness (F)''' of a '''class <math> C_i</math>''' is defined as the '''actual number of instances''' that belong to the subtree rooted at <math>C_i (C_i (I))</math> compared to the '''expected number of instances''' that belong to the subtree rooted at <math>C_i (C_i'(I))</math>. |
<math>F=\frac{|C_i (I)|}{C_i'(I)}</math> | <math>F=\frac{|C_i (I)|}{C_i'(I)}</math> | ||
The result of the formula will be a percentage representing the actual coverage of instances compared to the expected coverage. In most cases, this measure is an indication of how well the instance extraction process performed. For example, a knowledgebase where most classes have a low F would require more data extraction. On the other hand, a knowledgebase where most classes are almost full would indicate that it reflects more closely the knowledge encoded in the schema. | The result of the formula will be a percentage representing the actual coverage of instances compared to the expected coverage. In most cases, this measure is an indication of how well the instance extraction process performed. For example, a knowledgebase where most classes have a low F would require more data extraction. On the other hand, a knowledgebase where most classes are almost full would indicate that it reflects more closely the knowledge encoded in the schema. | ||
| + | |||
| + | [[Class_Metrics#Sources | Source 2]] | ||
==Class Importance== | ==Class Importance== | ||
| Line 22: | Line 26: | ||
This metric calculates the percentage of instances that belong to classes at the inheritance subtree rooted at the current class with respect to the total number of instances. This metric is important in that it will help in identifying which areas of the schema are in focus when the instances are added to the knowledgebase. Although this measure doesn’t consider the domain characteristics, it can still be used to give an idea on what parts of the ontology are considered focal and what parts are on the edges. | This metric calculates the percentage of instances that belong to classes at the inheritance subtree rooted at the current class with respect to the total number of instances. This metric is important in that it will help in identifying which areas of the schema are in focus when the instances are added to the knowledgebase. Although this measure doesn’t consider the domain characteristics, it can still be used to give an idea on what parts of the ontology are considered focal and what parts are on the edges. | ||
| − | The importance of a class <math>(Imp(C_i))</math> is defined as the percentage of the number of instances that belong to the inheritance subtree rooted at <math>C_i</math> in the | + | The '''importance of a class''' <math>(Imp(C_i))</math> is defined as the '''percentage of the number of instances''' that belong to the inheritance subtree rooted at <math>C_i</math> in the knowledgebase <math>(inst(C_i))</math> compared to the '''total number of class instances in the knowledgebase''' <math>KB(CI)</math>. |
<math>Imp(Ci)=\frac{|INST(Ci)|}{|KB(CI)|}</math> | <math>Imp(Ci)=\frac{|INST(Ci)|}{|KB(CI)|}</math> | ||
| + | |||
| + | [[Class_Metrics#Sources | Source 1]] | ||
==Class Inheritance Richness== | ==Class Inheritance Richness== | ||
| − | This measure details the schema | + | This measure details the schema IR metric mentioned in [[Schema_Metrics | schema metrics]] and describes the distribution of information in the current class subtree per class. This measure is a good indication of how well knowledge is grouped into different categories and subcategories under this class. |
| − | Formally, the inheritance richness ( | + | Formally, the '''inheritance richness (IRc) of class''' <math>C_i</math> is defined as the '''average number of subclasses per class''' in the subtree. The '''number of subclasses for a class''' <math>C_i</math> is defined as <math>|H^C(C_1,C_i)|</math> and the '''number of nodes in the subtree''' is |C'|. |
| − | <math> | + | <math>IRc = \frac{\sum_{Cj\in C'} |H^C(C1,Ci)|}{|C'|}</math> |
The result of the formula will be a real number representing the average number of classes per schema level. The interpretation of the results of this metric depends highly on the nature of the ontology. Classes in an ontology that represents a very specific domain will have low IRC values, while classes in an ontology that represents a wide domain will usually have higher IRC values. | The result of the formula will be a real number representing the average number of classes per schema level. The interpretation of the results of this metric depends highly on the nature of the ontology. Classes in an ontology that represents a very specific domain will have low IRC values, while classes in an ontology that represents a wide domain will usually have higher IRC values. | ||
| + | [[Class_Metrics#Sources | Source 2]] | ||
==Class Readability== | ==Class Readability== | ||
| − | This metric indicates the existence of human readable descriptions in the ontology, such as comments, labels, or captions. This metric can be a good indication if the ontology is going to be queried and the results listed to users. Formally, the '''readability (Rd)''' of a class <math>C_i</math> is defined as the '''sum of the number attributes that are comments and the number of attributes that are labels''' the class has. | + | This metric indicates the existence of human readable descriptions in the ontology, such as comments, labels, or captions. This metric can be a good indication if the ontology is going to be queried and the results listed to users. Formally, the '''readability (Rd)''' of a class <math>C_i</math> is defined as the '''sum of the number of attributes that are comments and the number of attributes that are labels''' the class has. |
<math> Rd = |A, A = rdfs:comment| + |A, A=refs:label|</math> | <math> Rd = |A, A = rdfs:comment| + |A, A=refs:label|</math> | ||
The result of the formula will be an integer representing the availability of human-readable information for the instances of the current class. | The result of the formula will be an integer representing the availability of human-readable information for the instances of the current class. | ||
| + | |||
| + | [[Class_Metrics#Sources | Source 1]] | ||
==Class Relationship Richness== | ==Class Relationship Richness== | ||
| Line 49: | Line 58: | ||
This is an important metric reflecting how much of the relationships defined for the class in the schema are actually being used at the instances level. This is another good indication of the utilization of the knowledge modelled in the schema. | This is an important metric reflecting how much of the relationships defined for the class in the schema are actually being used at the instances level. This is another good indication of the utilization of the knowledge modelled in the schema. | ||
| − | The '''relationship richness (RR)''' of a class <math>C_i</math> is defined as the percentage of the number of relationships that are being used by instances <math>I_i</math> that belong to <math>C_i (P(I_i,I_j))</math> compared to the number of relationships that are defined for <math>C_i</math> at the schema level <math>(P(C_i,C_j))</math>. | + | The '''relationship richness (RR)''' of a class <math>C_i</math> is defined as the '''percentage of the number of relationships''' that are being used by instances <math>I_i</math> that belong to <math>C_i (P(I_i,I_j))</math> compared to the '''number of relationships''' that are defined for <math>C_i</math> at the schema level <math>(P(C_i,C_j))</math>. |
| + | |||
| + | [[Class_Metrics#Sources | Source 2]] | ||
| + | |||
| + | ==Class children== | ||
| + | This count-metric measures the number of immediate descendants of the given class, also known as a number of children (NOC). | ||
| + | |||
| + | ==Class instances== | ||
| + | Displays the number of instances of a given class. OWL classes provide an abstraction mechanism for grouping resources with similar characteristics. Like RDF classes, every OWL class is associated with a set of individuals, called the class extension. The individuals in the class extension are called the instances of the class. A class has an intensional meaning (the underlying concept) which is related but not equal to its class extension. Thus, two classes may have the same class extension, but still be different classes. | ||
| + | |||
| + | ==Class properties== | ||
| + | Summarize the properties of an given class. Properties can be used to state relationships between individuals or from individuals to data values. Examples of properties include hasChild, hasRelative, hasSibling, and hasAge. The first three can be used to relate an instance of a class Person to another instance of the class Person (and are thus occurences of ObjectProperty), and the last (hasAge) can be used to relate an instance of the class Person to an instance of the datatype Integer (and is thus an occurence of DatatypeProperty). Both owl:ObjectProperty and owl:DatatypeProperty are subclasses of the RDF class rdf:Property. | ||
==Sources== | ==Sources== | ||
| − | #''Samir Tartir, I. Budak Arpinar, Amit P. Sheth: Ontological Evaluation and Validation <br /> In: Theory and Applications of Ontology: Computer Applications 2010, pp 115-130<br /> http://link.springer.com/chapter/10.1007%2F978-90-481-8847-5_5 | + | #''Samir Tartir, I. Budak Arpinar, Amit P. Sheth: Ontological Evaluation and Validation <br /> In: Theory and Applications of Ontology: Computer Applications 2010, pp 115-130.<br /> http://link.springer.com/chapter/10.1007%2F978-90-481-8847-5_5 |
| − | #''Samir Tartir, I. Budak Arpinar, Michael Moore, Amit P. Sheth, and Boanerges Aleman-meza: <br />Ontoqa: Metric-based ontology quality analysis. <br />In: IEEE Workshop on Knowledge Acquisition from Distributed, Autonomous, Semantically Heterogeneous Data and Knowledge Sources, 2005. <br />http://cobweb.cs.uga.edu/~budak/papers/ontoqa.pdf | + | #''Samir Tartir, I. Budak Arpinar, Michael Moore, Amit P. Sheth, and Boanerges Aleman-meza: <br />Ontoqa: Metric-based ontology quality analysis. <br />In: IEEE Workshop on Knowledge Acquisition from Distributed, Autonomous, Semantically Heterogeneous Data and Knowledge Sources, 2005, pp 4-6. <br />http://cobweb.cs.uga.edu/~budak/papers/ontoqa.pdf |
| + | #''http://gromit.iiar.pwr.wroc.pl/p_inf/ckjm/metric.html'' | ||
| + | #''http://www.infowebml.ws/rdf-owl/Class-owl.htm'' | ||
| + | #''https://www.w3.org/TR/2004/REC-owl-features-20040210/#property'' | ||
Latest revision as of 00:10, 11 September 2016
Class Metrics examine the classes and relationships of ontologies.
Contents
Class Connectivity
This metric is intended to give an indication of what classes are central in the ontology based on the instance relationship graph (where nodes represent instances and edges represent the relationships between them). This measure works in tandem with the importance metric mentioned next to create a better understanding of how focal some classes function. This measure can be used to understand the nature of the ontology by indicating which classes play a central role compared to other classes.
The connectivity of a class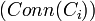 
is defined as the total number of relationships instances of the class have with instances of other classes (NIREL).
Class Fullness
This metric details the knowledgebase average population metric which are part of the knowledgebase metrics. It would be mainly used by an ontology developer interested in knowing how well the data extraction was with respect to the expected number of instances of each class. This is helpful in directing the extraction process to any resources that will add instances belonging to classes that are not full.
Formally, the fullness (F) of a class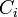 
is defined as the actual number of instances that belong to the subtree rooted at 
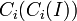compared to the expected number of instances that belong to the subtree rooted at 
.
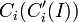The result of the formula will be a percentage representing the actual coverage of instances compared to the expected coverage. In most cases, this measure is an indication of how well the instance extraction process performed. For example, a knowledgebase where most classes have a low F would require more data extraction. On the other hand, a knowledgebase where most classes are almost full would indicate that it reflects more closely the knowledge encoded in the schema.
Class Importance
This metric calculates the percentage of instances that belong to classes at the inheritance subtree rooted at the current class with respect to the total number of instances. This metric is important in that it will help in identifying which areas of the schema are in focus when the instances are added to the knowledgebase. Although this measure doesn’t consider the domain characteristics, it can still be used to give an idea on what parts of the ontology are considered focal and what parts are on the edges.
The importance of a class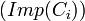 
is defined as the percentage of the number of instances that belong to the inheritance subtree rooted at 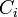in the knowledgebase 
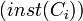compared to the total number of class instances in the knowledgebase 
.
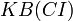Class Inheritance Richness
This measure details the schema IR metric mentioned in schema metrics and describes the distribution of information in the current class subtree per class. This measure is a good indication of how well knowledge is grouped into different categories and subcategories under this class.
Formally, the inheritance richness (IRc) of class 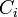is defined as the average number of subclasses per class in the subtree. The number of subclasses for a class 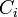is defined as 
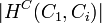and the number of nodes in the subtree is |C'|.
The result of the formula will be a real number representing the average number of classes per schema level. The interpretation of the results of this metric depends highly on the nature of the ontology. Classes in an ontology that represents a very specific domain will have low IRC values, while classes in an ontology that represents a wide domain will usually have higher IRC values.
Class Readability
This metric indicates the existence of human readable descriptions in the ontology, such as comments, labels, or captions. This metric can be a good indication if the ontology is going to be queried and the results listed to users. Formally, the readability (Rd) of a class 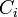is defined as the sum of the number of attributes that are comments and the number of attributes that are labels the class has.
The result of the formula will be an integer representing the availability of human-readable information for the instances of the current class.
Class Relationship Richness
This is an important metric reflecting how much of the relationships defined for the class in the schema are actually being used at the instances level. This is another good indication of the utilization of the knowledge modelled in the schema.
The relationship richness (RR) of a class 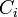is defined as the percentage of the number of relationships that are being used by instances 
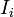that belong to 
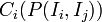compared to the number of relationships that are defined for 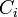at the schema level 
.
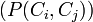Class children
This count-metric measures the number of immediate descendants of the given class, also known as a number of children (NOC).
Class instances
Displays the number of instances of a given class. OWL classes provide an abstraction mechanism for grouping resources with similar characteristics. Like RDF classes, every OWL class is associated with a set of individuals, called the class extension. The individuals in the class extension are called the instances of the class. A class has an intensional meaning (the underlying concept) which is related but not equal to its class extension. Thus, two classes may have the same class extension, but still be different classes.
Class properties
Summarize the properties of an given class. Properties can be used to state relationships between individuals or from individuals to data values. Examples of properties include hasChild, hasRelative, hasSibling, and hasAge. The first three can be used to relate an instance of a class Person to another instance of the class Person (and are thus occurences of ObjectProperty), and the last (hasAge) can be used to relate an instance of the class Person to an instance of the datatype Integer (and is thus an occurence of DatatypeProperty). Both owl:ObjectProperty and owl:DatatypeProperty are subclasses of the RDF class rdf:Property.
Sources
- Samir Tartir, I. Budak Arpinar, Amit P. Sheth: Ontological Evaluation and Validation
In: Theory and Applications of Ontology: Computer Applications 2010, pp 115-130.
http://link.springer.com/chapter/10.1007%2F978-90-481-8847-5_5 - Samir Tartir, I. Budak Arpinar, Michael Moore, Amit P. Sheth, and Boanerges Aleman-meza:
Ontoqa: Metric-based ontology quality analysis.
In: IEEE Workshop on Knowledge Acquisition from Distributed, Autonomous, Semantically Heterogeneous Data and Knowledge Sources, 2005, pp 4-6.
http://cobweb.cs.uga.edu/~budak/papers/ontoqa.pdf - http://gromit.iiar.pwr.wroc.pl/p_inf/ckjm/metric.html
- http://www.infowebml.ws/rdf-owl/Class-owl.htm
- https://www.w3.org/TR/2004/REC-owl-features-20040210/#property
