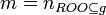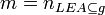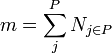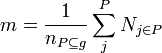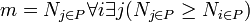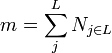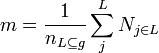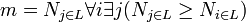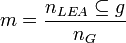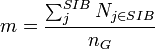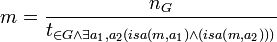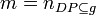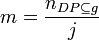Difference between revisions of "Graph Metrics"
Adminofwiki (Talk | contribs) |
Adminofwiki (Talk | contribs) |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Graph or structural metrics calculate the structure of ontologies. | |
| − | == | + | ==Cardinality== |
| + | Cardinality is a property of graphs which expresses a graph related number of specific elements. | ||
| − | + | ===Absolute root cardinality=== | |
| − | + | Absolute root cardinality is a property of a directed graph which represents the number of root nodes of the graph. | |
| − | = | + | <math>m = n_{ROO \subseteq g}</math> |
| − | + | <math>n_{ROO \subseteq g}</math> is the cardinality of the set <math>ROO</math> in the directed graph <math>g</math>. | |
| − | + | ||
| − | |||
| − | + | ===Absolute leaf cardinality=== | |
| − | The | + | Absolute root cardinality is a property of a directed graph which is related to leaf node sets and represents the number of leaf nodes of the graph. |
| + | |||
| + | <math>m = n_{LEA \subseteq g}</math> | ||
| + | |||
| + | <math>n_{LEA \subseteq g}</math> is the cardinality of the set <math>LEA</math> in the directed graph <math>g</math>. | ||
| + | |||
| + | |||
| + | ===Absolute sibling cardinality=== | ||
| + | Absolute root cardinality is a property of a directed graph which is related to sibling node sets and represents the number of sibling nodes of the graph. | ||
| + | |||
| + | <math>\sum_{j}^{SIB} N_{j \in SIB}</math> | ||
| + | |||
| + | <math>N_{j \in SIB}</math> is the cardinality of a sibling set <math>j</math> from <math>SIB</math> in the graph <math>g</math>. | ||
| + | |||
| + | |||
| + | ==Depth== | ||
| + | Depth is a property of graphs which is related to cardinality of paths existing in the graph. The arcs which are considered are only subClassOf (isa) arcs but this only applies to directed graphs. | ||
| + | |||
| + | ===Absolute depth=== | ||
| + | The value of the absolute depth is calculated as follows: | ||
| + | |||
| + | <math>m = \sum_{j}^P N_{j \in P}</math> | ||
| + | |||
| + | <math>N_{j \in P}</math> is the cardinality of each path <math>j</math> from the set of paths <math>P</math> in a graph <math>g</math>. | ||
| + | |||
| + | |||
| + | ===Average depth=== | ||
| + | The average depth states at which degree the ontology has a vertical modelling of hierarchies. | ||
| + | |||
| + | <math>m = \frac{1}{n_{P \subseteq g}} \sum_{j}^P N_{j \in P}</math> | ||
| + | |||
| + | <math>N_{j \in P}</math> is the cardinality of each path <math>j</math> from the set of paths <math>P</math> in a graph <math>g</math> and <math>n_{P \subseteq g}</math> is the cardinality of <math>P</math>. | ||
| + | |||
| + | |||
| + | ===Maximal depth=== | ||
| + | The height of a graph is its maximal depth and it is the result of the following: | ||
| + | |||
| + | <math>m = N_{j \in P} | ||
| + | \forall i \exists j (N_{j \in P} \geq N_{i \in P})</math> | ||
| + | |||
| + | <math>N_{i \in P}</math> and <math>N_{j \in P}</math> is the cardinality of each path <math>j</math> from the set of paths <math>P</math> in a graph <math>g</math>. | ||
| + | |||
| + | |||
| + | ==Breadth== | ||
| + | Here are again only subClassOf (isa) arcs considered to get a property called breadth which is related to the cardinality of levels, so-called generations, in a directed graph. | ||
| + | |||
| + | ===Absolute breadth=== | ||
| + | The value of the absolute breadth is calculated as follows: | ||
| + | |||
| + | <math>m = \sum_{j}^L N_{j \in L}</math> | ||
| + | |||
| + | <math>N_{j \in L}</math> is the cardinality of each level/generation <math>j</math> from the set of generations <math>L</math> in a directed graph <math>g</math>. | ||
| + | |||
| + | |||
| + | ===Average breadth=== | ||
| + | The average breadth states at which degree the ontology has a horizontal modelling of hierarchies. | ||
| + | |||
| + | <math>m = \frac{1}{n_{L \subseteq g}} \sum_{j}^L N_{j \in L}</math> | ||
| + | |||
| + | <math>N_{j \in L}</math> is the cardinality of each generation <math>j</math> from the set of generations <math>L</math> in a directed graph <math>g</math> and <math>n_{L \subseteq g}</math> is the cardinality of <math>L</math>. | ||
| + | |||
| + | |||
| + | ===Maximal breadth=== | ||
| + | The maximal breadth of a directed graph is calculated the following way: | ||
| + | |||
| + | <math>m = N_{j \in L} | ||
| + | \forall i \exists j (N_{j \in L} \geq N_{i \in L})</math> | ||
| + | |||
| + | <math>N_{i \in L}</math> and <math>N_{j \in L}</math> is the cardinality of each generation <math>j</math> from the set of generations <math>L</math> in a graph <math>g</math>. | ||
| + | |||
==Fan-outness== | ==Fan-outness== | ||
| + | Fan-outness is related to the “dispersion” of graph nodes. The arcs considered for this property are again subClassOf (isa) arcs. There are two different measures which can be distinguished: those which are related to leaf node set, like the following ratio of leaf fan-outness, and those which are related to sibling node sets ("internal dispersion"), like the following ratio of sibling fan-outness. | ||
| + | |||
| + | ===Ratio of leaf fan-outness=== | ||
| + | The ratio of leaf fan-outness is the result of the absolute leaf cardinality divided by the cardinality of the graph. | ||
| + | |||
| + | <math>m = \frac{n_{LEA} \subseteq g}{n_G}</math> | ||
| + | |||
| + | <math>n_{LEA} \subseteq g</math> is the cardinality of the set <math>LEA</math> in a directed graph <math>g</math> and <math>n_G</math> is the cardinality of <math>G</math>. | ||
| + | |||
| + | |||
| + | ===Ratio of sibling fan-outness=== | ||
| + | The ratio of sibling fan-outness is the result of the absolute sibling cardinality divided by the cardinality of the graph. | ||
| + | |||
| + | <math>m = \frac{\sum_{j}^{SIB} N_{j \in SIB}}{n_G}</math> | ||
| + | |||
| + | <math>\sum_{j}^{SIB} N_{j \in SIB}</math> is the absolute sibling cardinality for the directed graph <math>g</math> and <math>n_G</math> is the cardinality of <math>G</math>. | ||
| + | |||
| + | |||
| + | ==Tangledness== | ||
| + | |||
| + | Tangledness is related to the multihierarchical nodes of a graph, where the arcs considered here are again only subClassOf (isa) arcs and the measure again only applies to directed graphs. | ||
| + | The tangledness of a class tree is subject of multiple hierarchy knots of a graph. It means, that this knot has more than one incoming edge. This is the formula for this measurement: | ||
| + | |||
| + | <math>m = \frac{n_G}{t_{\in G \wedge \exists a_1 ,a_2 (isa(m,a_1 )\wedge (isa(m,a_2)))}}</math> | ||
| + | |||
| + | <math>n_G</math> is the cardinality of <math>G</math> and <math>t_{\in G \wedge \exists a_1 ,a_2 (isa(m,a_1 )\wedge (isa(m,a_2)))}</math> is the cardinality of the set of nodes with more than one ingoing subClassOf (isa) arc in <math>g</math>. | ||
| + | |||
| + | |||
| + | ==Total number of paths== | ||
| + | The total number of paths is the sum of distinct paths which exists in (set of) graphs where each path start at a root node and ends at a leaf node. | ||
| + | |||
| + | <math>m = n_{DP \subseteq g}</math> | ||
| + | |||
| + | <math>n_{DP \subseteq g}</math> is the cardinality of the set <math>DP</math> in the directed graph <math>g</math>. | ||
| + | |||
| + | |||
| + | ==Average number of paths== | ||
| + | The average number of paths is the quotient of the total number of distinct paths and the number of graphs. | ||
| + | |||
| + | <math>m = \frac{n_{DP \subseteq g}}{j}</math> | ||
| + | |||
| + | <math>n_{DP \subseteq g}</math> is the cardinality of the set <math>DP</math> in the directed graphs <math>g</math> and the number of graphs <math>j</math>. | ||
| − | |||
==Density== | ==Density== | ||
| Line 25: | Line 134: | ||
To detect those areas, there are already several classifying techniques existing to be able to measure the absolute size and quantity. | To detect those areas, there are already several classifying techniques existing to be able to measure the absolute size and quantity. | ||
| − | + | ''This metric is not implemented in the ontometrics project yet.'' | |
| − | |||
==Logical Adequacy== | ==Logical Adequacy== | ||
| − | The logical | + | The logical adequacy of a graph is described by formal semantics where either directed or conceptual relations exist. Consistency ratio can be derived from it with 'nInc' of quantity cardinality from consistent classes of the graph 'g' and 'nG' of quantity cardinality from class knots of the graph 'g'. |
| + | ''This metric is not implemented in the ontometrics project yet.'' | ||
| − | |||
| − | + | ==Modularity== | |
| − | + | ||
| − | + | Modularity is related to the asserted modules of a graph, where the arcs considered here are either subClassOf or non-subClassOf arcs. In comparison to cohesion, the number of knots of connected components are put into proportion to the number of all graph elements. However, basically they describe equivalent metrics. | |
| − | + | ||
| + | ''This metric is not implemented in the ontometrics project yet.'' | ||
| + | |||
| + | |||
| + | ==Sources== | ||
| − | + | #''Aldo Gangemi, Carola Catenacci, Massimiliano Ciaramita, Jos Lehmann:<br /> Ontology evaluation and validation - An integrated formal model for the quality diagnostic task<br /> September 2005 , pp 11-16. <br />http://www.loa.istc.cnr.it/old/Files/OntoEval4OntoDev_Final.pdf'' | |
| − | + | ||
Latest revision as of 23:42, 10 September 2016
Graph or structural metrics calculate the structure of ontologies.
Contents
Cardinality
Cardinality is a property of graphs which expresses a graph related number of specific elements.
Absolute root cardinality
Absolute root cardinality is a property of a directed graph which represents the number of root nodes of the graph.
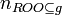 is the cardinality of the set
is the cardinality of the set 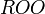 in the directed graph
in the directed graph 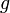 .
.
Absolute leaf cardinality
Absolute root cardinality is a property of a directed graph which is related to leaf node sets and represents the number of leaf nodes of the graph.
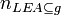 is the cardinality of the set
is the cardinality of the set 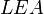 in the directed graph
in the directed graph 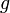 .
.
Absolute sibling cardinality
Absolute root cardinality is a property of a directed graph which is related to sibling node sets and represents the number of sibling nodes of the graph.
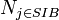 is the cardinality of a sibling set
is the cardinality of a sibling set 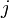 from
from 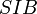 in the graph
in the graph 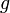 .
.
Depth
Depth is a property of graphs which is related to cardinality of paths existing in the graph. The arcs which are considered are only subClassOf (isa) arcs but this only applies to directed graphs.
Absolute depth
The value of the absolute depth is calculated as follows:
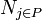 is the cardinality of each path
is the cardinality of each path 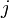 from the set of paths
from the set of paths 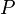 in a graph
in a graph 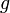 .
.
Average depth
The average depth states at which degree the ontology has a vertical modelling of hierarchies.
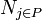 is the cardinality of each path
is the cardinality of each path 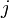 from the set of paths
from the set of paths 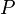 in a graph
in a graph 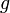 and
and 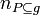 is the cardinality of
is the cardinality of 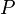 .
.
Maximal depth
The height of a graph is its maximal depth and it is the result of the following:
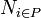 and
and 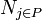 is the cardinality of each path
is the cardinality of each path 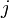 from the set of paths
from the set of paths 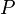 in a graph
in a graph 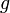 .
.
Breadth
Here are again only subClassOf (isa) arcs considered to get a property called breadth which is related to the cardinality of levels, so-called generations, in a directed graph.
Absolute breadth
The value of the absolute breadth is calculated as follows:
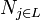 is the cardinality of each level/generation
is the cardinality of each level/generation 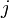 from the set of generations
from the set of generations 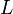 in a directed graph
in a directed graph 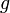 .
.
Average breadth
The average breadth states at which degree the ontology has a horizontal modelling of hierarchies.
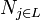 is the cardinality of each generation
is the cardinality of each generation 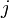 from the set of generations
from the set of generations 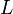 in a directed graph
in a directed graph 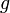 and
and 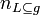 is the cardinality of
is the cardinality of 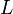 .
.
Maximal breadth
The maximal breadth of a directed graph is calculated the following way:
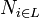 and
and 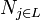 is the cardinality of each generation
is the cardinality of each generation 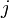 from the set of generations
from the set of generations 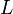 in a graph
in a graph 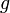 .
.
Fan-outness
Fan-outness is related to the “dispersion” of graph nodes. The arcs considered for this property are again subClassOf (isa) arcs. There are two different measures which can be distinguished: those which are related to leaf node set, like the following ratio of leaf fan-outness, and those which are related to sibling node sets ("internal dispersion"), like the following ratio of sibling fan-outness.
Ratio of leaf fan-outness
The ratio of leaf fan-outness is the result of the absolute leaf cardinality divided by the cardinality of the graph.
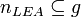 is the cardinality of the set
is the cardinality of the set 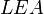 in a directed graph
in a directed graph 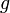 and
and 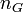 is the cardinality of
is the cardinality of 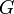 .
.
Ratio of sibling fan-outness
The ratio of sibling fan-outness is the result of the absolute sibling cardinality divided by the cardinality of the graph.
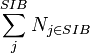 is the absolute sibling cardinality for the directed graph
is the absolute sibling cardinality for the directed graph 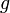 and
and 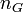 is the cardinality of
is the cardinality of 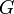 .
.
Tangledness
Tangledness is related to the multihierarchical nodes of a graph, where the arcs considered here are again only subClassOf (isa) arcs and the measure again only applies to directed graphs. The tangledness of a class tree is subject of multiple hierarchy knots of a graph. It means, that this knot has more than one incoming edge. This is the formula for this measurement:
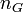 is the cardinality of
is the cardinality of 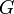 and
and 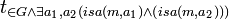 is the cardinality of the set of nodes with more than one ingoing subClassOf (isa) arc in
is the cardinality of the set of nodes with more than one ingoing subClassOf (isa) arc in 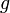 .
.
Total number of paths
The total number of paths is the sum of distinct paths which exists in (set of) graphs where each path start at a root node and ends at a leaf node.
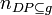 is the cardinality of the set
is the cardinality of the set 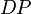 in the directed graph
in the directed graph 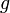 .
.
Average number of paths
The average number of paths is the quotient of the total number of distinct paths and the number of graphs.
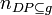 is the cardinality of the set
is the cardinality of the set 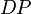 in the directed graphs
in the directed graphs 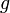 and the number of graphs
and the number of graphs 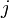 .
.
Density
Density can be defined as the presence of clusters of classes with many non-taxonomical relations holding among them. For example, so-called core ontology patterns (for thematic roles in events, contracts, diagnoses, etc.) usually constitute dense areas in an ontology. To detect those areas, there are already several classifying techniques existing to be able to measure the absolute size and quantity.
This metric is not implemented in the ontometrics project yet.
Logical Adequacy
The logical adequacy of a graph is described by formal semantics where either directed or conceptual relations exist. Consistency ratio can be derived from it with 'nInc' of quantity cardinality from consistent classes of the graph 'g' and 'nG' of quantity cardinality from class knots of the graph 'g'.
This metric is not implemented in the ontometrics project yet.
Modularity
Modularity is related to the asserted modules of a graph, where the arcs considered here are either subClassOf or non-subClassOf arcs. In comparison to cohesion, the number of knots of connected components are put into proportion to the number of all graph elements. However, basically they describe equivalent metrics.
This metric is not implemented in the ontometrics project yet.
Sources
- Aldo Gangemi, Carola Catenacci, Massimiliano Ciaramita, Jos Lehmann:
Ontology evaluation and validation - An integrated formal model for the quality diagnostic task
September 2005 , pp 11-16.
http://www.loa.istc.cnr.it/old/Files/OntoEval4OntoDev_Final.pdf