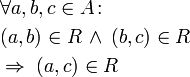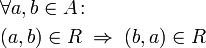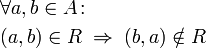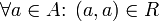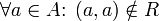Difference between revisions of "Object Property Axioms"

From OntoMetrics
Jump to: navigation, search
(→‎Transitive object property axioms count)
 
(20 intermediate revisions by the same user not shown)
Line 3: Line 3:
 
A set of instances connected to the property is called a property extension.
 
A set of instances connected to the property is called a property extension.
  
−
==SubObjectPropertyOf axioms count==
+
==SubObjectPropertyOf axiom==
  
−
This axiom says that a property is a subproperty of another property.
+
This axiom says that a property 'p1' is a subproperty 'sp1' of another property 'p2'.
 
It also means that the instances of the subproperty are subsets to the property extension of the second property.
 
It also means that the instances of the subproperty are subsets to the property extension of the second property.
  
−
This Axiom can equally be used on object properties and data properties.
+
==Equivalent object property axiom==
  
−
==Equivalent object property axioms count==
+
Equivalent property axioms exist, when two properties have the same property extension.
  
−
Equivalent property axioms exist when two properties have the same property extension.
+
==Inverse object properties axiom==
 +
Properties have a direction defined with domain to range, the 'inverseof' term is used to mirror the direction.
  
 
This Axiom can equally be used on object properties and data properties.
 
This Axiom can equally be used on object properties and data properties.
  
−
==Inverse object properties axioms count==
+
==Disjoint object properties axiom==
−
Properties have a direction defined with domain to range, the inverseof term is used to mirror the direction.
+
  
−
This Axiom can equally be used on object properties and data properties.
+
Two properties are disjoint when they don't have individuals in common.
  
−
==Disjoint object properties axioms count==
+
==Functional object properties axiom==
 +
A functional property is a property which can only have one value.
  
−
Two properties are disjoint when they don't have individuals in common.
 
  
−
==Functional object properties axioms count==
+
For an individual 'x', there can be only one definite individual 'y' such that 'x' is connected by the object property expression 'OPE' to 'y'.
−
A functional property is a property which can only have one value. E.g. a woman can have at most one husband.
+
  
−
This Axiom can equally be used on object properties and data properties.
+
For example:
 +
FunctionalObjectProperty( a:hasHusband )                 Each object can have at most one husband.
 +
ObjectPropertyAssertion( a:hasHusband a:Nicole a:Steve ) Steve is Nicole's husband.
  
 +
==Inverse functional object properties axiom==
 +
For an individual 'x', there can be at most one individual 'y' such that 'y' is connected by the object property expression 'OPE' with 'x'.
  
−
==Inverse functional object properties axioms count==
+
InverseFunctionalObjectProperty( a:hasHusband )         Each object can have at most one husband.
 +
ObjectPropertyAssertion( a:hasHusband a:Steve a:Nicole ) Steve is Nicole's husband.
  
−
==Transitive object property axioms count==
+
 
 +
==Transitive object property axiom==
 
Transitive means that if a property contains the pair(x,y)and the pair (y,z) then we can conclude that the pair(x,z) is also part of der property.
 
Transitive means that if a property contains the pair(x,y)and the pair (y,z) then we can conclude that the pair(x,z) is also part of der property.
  
Line 42: Line 47:
 
         \end{align}</math>
 
         \end{align}</math>
  
−
==Symmetric object property axioms count==
+
==Symmetric object property axiom==
  
 
If a property is symmetric it means that if a pair(x,y) exists, then there is also a pair (y,x).
 
If a property is symmetric it means that if a pair(x,y) exists, then there is also a pair (y,x).
  
−
==Asymmetric object property axioms count==
+
<math>\begin{align}
 +
            &\forall a,b \in A\colon\\
 +
            &(a,b) \in R \;\Rightarrow\; (b,a) \in R
 +
        \end{align}</math>
 +
 
 +
==Asymmetric object property axiom==
  
 
A asymmetric property has a pair(x,y) but never a pair(y,x).
 
A asymmetric property has a pair(x,y) but never a pair(y,x).
  
−
==Reflexive object property axioms count==
+
<math>\begin{align}
 +
            &\forall a,b \in A\colon\\
 +
            & (a,b) \in R \;\Rightarrow\; (b,a) \notin R
 +
        \end{align}</math>
  
−
Reflexiv means that a property relates to itself.
+
==Reflexive object property axiom==
  
−
<math>R</math> is ''reflexive'' :<math>\Longleftrightarrow \forall x \in M: xRx</math>
+
Reflexive means that a property relates to itself.
  
−
==Irreflexive object property axioms count==
+
<math>\forall a \in A\colon\; (a,a) \in R</math>
 +
 
 +
==Irreflexive object property axiom==
 
Subsequently irreflexive means that no individual relates to itself.
 
Subsequently irreflexive means that no individual relates to itself.
−
  <math>R</math> is ''irreflexive'' :<math>\Longleftrightarrow \forall x \in M: \neg \ xRx</math>
+
  <math>\forall a \in A\colon\; (a,a) \notin R</math>
−
 
+
−
==Object property domain axioms count==
+
−
The domain links a property to a class description.
+
−
 
+
−
There can be more than one domain for a property.
+
  
−
==Object property range axioms count==
+
==Object property domain axiom==
−
The range links the property to either a class description or a data range.
+
This axiom states that the domain of the object property expression is the class expression.
  
−
There can be more than one range for a property.
+
==Object property range axiom==
 +
This axiom states that the range of the object property expression is the class expression.
  
−
==SubPropertyChainOf axioms count==
+
==SubPropertyChainOf axiom==
  
−
These axioms are used to create a chain of multiple properties. E.g. two hasParents properties are linked by a chain thus a hasGrandparents property will be identified.
+
These axioms are used to create a chain of multiple properties. E.g. two 'hasParents' properties are linked by a chain thus a 'hasGrandparents' property will be identified.
  
 
==Sources==
 
==Sources==
−
#''https://www.w3.org/TR/owl-ref/#Property''
+
#''https://www.w3.org/TR/owl2-primer/#Object_Properties/''
−
#''https://www.w3.org/TR/owl2-primer/''
+
#''https://www.w3.org/TR/owl2-syntax/#Object_Property_Axioms''

Latest revision as of 23:01, 10 September 2016

Object properties link individuals to individuals.

A set of instances connected to the property is called a property extension.

SubObjectPropertyOf axiom

This axiom says that a property 'p1' is a subproperty 'sp1' of another property 'p2'. It also means that the instances of the subproperty are subsets to the property extension of the second property.

Equivalent object property axiom

Equivalent property axioms exist, when two properties have the same property extension.

Inverse object properties axiom

Properties have a direction defined with domain to range, the 'inverseof' term is used to mirror the direction.

This Axiom can equally be used on object properties and data properties.

Disjoint object properties axiom

Two properties are disjoint when they don't have individuals in common.

Functional object properties axiom

A functional property is a property which can only have one value.


For an individual 'x', there can be only one definite individual 'y' such that 'x' is connected by the object property expression 'OPE' to 'y'. 

For example:
FunctionalObjectProperty( a:hasHusband ) 	                Each object can have at most one husband.
ObjectPropertyAssertion( a:hasHusband a:Nicole a:Steve ) 	Steve is Nicole's husband.

Inverse functional object properties axiom

For an individual 'x', there can be at most one individual 'y' such that 'y' is connected by the object property expression 'OPE' with 'x'. 

InverseFunctionalObjectProperty( a:hasHusband ) 	        Each object can have at most one husband.
ObjectPropertyAssertion( a:hasHusband a:Steve a:Nicole ) 	Steve is Nicole's husband.


Transitive object property axiom

Transitive means that if a property contains the pair(x,y)and the pair (y,z) then we can conclude that the pair(x,z) is also part of der property. 

\begin{align}
            &\forall a,b,c \in A\colon\\
            &(a,b) \in R \,\land\, (b,c) \in R\\
            &\Rightarrow\; (a,c) \in R
        \end{align}

Symmetric object property axiom

If a property is symmetric it means that if a pair(x,y) exists, then there is also a pair (y,x). 

\begin{align}
            &\forall a,b \in A\colon\\
            &(a,b) \in R \;\Rightarrow\; (b,a) \in R
        \end{align}

Asymmetric object property axiom

A asymmetric property has a pair(x,y) but never a pair(y,x). 

\begin{align}
            &\forall a,b \in A\colon\\
            & (a,b) \in R \;\Rightarrow\; (b,a) \notin R
        \end{align}

Reflexive object property axiom

Reflexive means that a property relates to itself. 

\forall a \in A\colon\; (a,a) \in R

Irreflexive object property axiom

Subsequently irreflexive means that no individual relates to itself. 

\forall a \in A\colon\; (a,a) \notin R

Object property domain axiom

This axiom states that the domain of the object property expression is the class expression.

Object property range axiom

This axiom states that the range of the object property expression is the class expression.

SubPropertyChainOf axiom

These axioms are used to create a chain of multiple properties. E.g. two 'hasParents' properties are linked by a chain thus a 'hasGrandparents' property will be identified.

Sources

  1. https://www.w3.org/TR/owl2-primer/#Object_Properties/
  2. https://www.w3.org/TR/owl2-syntax/#Object_Property_Axioms
Retrieved from "http://ontometrics.informatik.uni-rostock.de:80/wiki/index.php?title=Object_Property_Axioms&oldid=306"